Expanding the Boundaries of Physics
When the Royal Swedish Academy of Sciences awarded the 2024 Nobel Prize in Physics to John J. Hopfield and Geoffrey E. Hinton, many were caught off guard. These researchers built their reputations in the domains of neural networks and machine learning—areas more often associated with computer science and cognitive science than with physics. Yet, by selecting them, the Academy highlighted how modern physics can include insights drawn from statistical mechanics, thermodynamics, and complex systems theory, and then apply these insights to understanding how information can be represented and learned. Far from the traditional images of colliding particles or orbiting planets, their work deals with patterns, states, and probabilities, but its theoretical roots and guiding principles come directly from physics.
Physics as a Source of Concepts for Learning Machines
For much of its history, physics focused on describing matter and energy with clear mathematical laws, often at a fundamental level. Over time, however, physicists have tackled ever more complex phenomena, sometimes involving large collections of interacting elements that cannot be fully described by simple equations. Statistical mechanics—a branch of physics developed in the late 19th and early 20th centuries—provided tools to handle these complex systems. It introduced energy functions, probability distributions over states, and equilibrium concepts that help us understand how properties of large ensembles emerge from interactions among individual parts.
It was this perspective that Hopfield and Hinton applied to neural networks. Artificial neural networks are collections of simple units, or “neurons,” connected by adjustable weights. The challenge is to find a way to set these weights so that the network can learn patterns, store memories, or model data. Hopfield and Hinton showed that principles from statistical physics, such as seeking states of minimum energy or following probability distributions shaped by an energy landscape, are directly applicable to these computational problems. By doing so, they built a bridge between physical intuition and computational learning.
Hopfield Networks: Energy Functions and Associative Memory
In the early 1980s, John J. Hopfield, originally trained as a physicist, proposed a class of neural networks now known as Hopfield networks. A Hopfield network is made up of binary neurons, each of which can be in one of two states, often represented as +1 or -1. Every pair of neurons i and j has a connection weight wij, and each neuron may also have a bias term. The network’s energy function, a key concept borrowed from physics, is defined as:
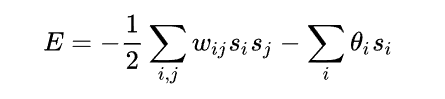
where si represents the state of neuron i and θi is a bias term that can shift the neuron’s preferred state. Typically, the weights are symmetric (wij=wji) and there are no self-connections (wii=0).
This energy function is similar to those found in models of magnetic materials, where spins can point up or down. Just as a physical system tends toward states of lower energy, a Hopfield network evolves its neuron states until it settles into a stable, low-energy configuration. Hopfield showed that if the weights are chosen according to specific learning rules—essentially correlating pairs of neurons that should be active together—these stable configurations can store memories. Presenting a part of a stored pattern as input nudges the network to converge on the full pattern, achieving a form of associative memory. In other words, the system uses physics-inspired energy minimization to retrieve a complete memory from incomplete cues.
This connection between neural networks and physical energy landscapes was a breakthrough. It placed computation in a familiar physical context: learning corresponded to sculpting an energy landscape so that certain patterns lie in deep “wells,” and recall involved rolling downhill into one of those wells. This analogy made it easier to analyze, understand, and eventually improve neural network models.
Hinton’s Boltzmann Machines: Probabilistic Models and Learning from Data
Around the same period, Geoffrey E. Hinton, trained in psychology and computer science but deeply influenced by the ideas of statistical physics, introduced another class of neural networks known as Boltzmann machines. These networks also contain units that can be in binary states, but they incorporate a probabilistic approach inspired by the Boltzmann distribution from thermodynamics. Instead of settling deterministically into the lowest-energy state, a Boltzmann machine explores many states with probabilities governed by the energy function. The energy of a Boltzmann machine configuration can be written as:

where si is the state of neuron i and bi is a bias for that neuron. The probability of the system being in state s is given by the Boltzmann distribution:
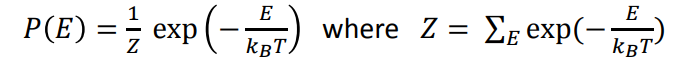
where T is a parameter analogous to temperature, kB is Boltzmann’s constant, and Z is a normalization factor (partition function) that ensures all probabilities sum to one.
When “learning” from data, a Boltzmann machine adjusts its weights so that the probability distribution represented by the network matches the distribution of observed data. Learning involves a two-step process: first, measure how often features occur together in real data, and then compare this to how often they occur in states sampled from the model. By adjusting weights to reduce any differences, the model gradually improves its internal representation of the data. This process requires sampling many states, akin to a physical system exploring its energy landscape, and pushing the network toward a distribution that captures the structure of the input data.
Hinton’s contribution lay in showing that these statistical physics principles—using probability distributions over configurations, adjusting weights to match observed statistics, and viewing the network as a system that can fluctuate among states—offer a powerful approach to machine learning. His Boltzmann machines provided a blueprint for building models that do not just store patterns but learn entire probability distributions. This concept became central to many later developments in machine learning, including deep learning methods that underlie many present-day applications.
From Theory to Practice
When Hopfield and Hinton first introduced these ideas, computers were slow, data scarce, and interest mostly academic. Hopfield networks and Boltzmann machines were small and not always practical. Yet their formulations built on solid physical and mathematical foundations, and that durability allowed these ideas to influence more advanced methods. As computing power grew and large datasets became available, researchers refined these concepts into more tractable forms.
One of the key refinements was the development of “restricted Boltzmann machines” (RBMs), a simplified version of the Boltzmann machine. RBMs removed certain connections to make learning faster and more stable. Stacking multiple RBMs led to “deep belief networks,” which helped kickstart the modern deep learning revolution. Although today’s deep learning systems often rely on gradient-based methods like backpropagation rather than pure Boltzmann machine training, the underlying idea that a network can learn complex distributions, guided by principles resembling statistical physics, never disappeared.
Applying These Methods in Physics
As the field of machine learning advanced, physicists began to realize that these tools could help solve problems once thought too complex for direct analytical methods. Particle physics experiments, such as those at the Large Hadron Collider, generate enormous volumes of data every second. Identifying subtle patterns—rare particle decays or unexpected anomalies—requires sifting through this data in ways that human analysts or simple formulas cannot match. Neural networks, building on Hopfield’s and Hinton’s foundational ideas, can rapidly classify events, detect anomalies, and find meaningful structures hidden in noise.
In quantum physics, many-body systems can be so complicated that writing down an exact wavefunction is impossible for large numbers of particles. Machine learning methods, often informed by energy-based or probabilistic models, can approximate these wavefunctions numerically. By treating the wavefunction as something that can be learned (much like a probability distribution in a Boltzmann machine), researchers can find more efficient ways to describe and simulate quantum states. This opens paths to tackling quantum problems that were once out of reach.
Materials science also benefits. Predicting the properties of a new material before synthesizing it is a complex challenge. Neural networks can learn patterns relating a material’s structure to its properties, guiding experimentalists in selecting candidates worth exploring in the lab. This reduces trial and error and speeds up innovation.
A Subtle Redefinition of Physics
Some critics question whether awarding the Nobel Prize in Physics to scholars whose primary reputation lies in neural networks stretches the definition of physics. Yet, the methods Hopfield and Hinton created are grounded in physical thinking. The analogy to energy landscapes, the probabilistic distributions drawn from thermodynamics, and the idea of equilibrium states are all directly borrowed from physics. Their networks represent a fusion of physical intuition with computational goals. This did not merely apply physics to another field; it advanced physics by providing a broader set of conceptual tools that can handle complexity and uncertainty.
Their work teaches that physics need not only be about particles, forces, and fields. It can also involve frameworks that treat information, patterns, and learning as physical processes with energy functions and probability distributions. These methods help physicists unravel problems where the complexity resists simple closed-form solutions. The Nobel Committee’s recognition underscores that physics can embrace such methods, and that doing so expands the frontiers of what physics can tackle.
Looking to the Future
The legacy of Hopfield and Hinton’s work is not just in the tools we have today, but in how it encourages physicists to think. Future physicists will likely see machine learning as a standard part of their training, as essential as differential equations or experimental design. They will treat large datasets from particle detectors, gravitational wave observatories, and quantum experiments not as insurmountable challenges, but as problems well-suited to methods that Hopfield and Hinton pioneered. They will also recognize the importance of understanding the energy landscapes and probability distributions that govern complex systems, whether those systems are collections of neurons, atoms, or spins.
At the same time, Hopfield and Hinton’s achievements raise important questions about how these tools are used. As machine learning systems become embedded in everyday life, questions about fairness, bias, and unintended consequences arise. Although these concerns extend beyond physics, the Nobel Prize acknowledges that these computational tools are now part of the physicist’s world. Physicists can no longer ignore how their methods might be used, or misused, outside the lab.
A Balanced Legacy
John J. Hopfield and Geoffrey E. Hinton’s contributions began with an effort to understand how simple models of interconnected units could store and recall patterns, or learn statistical structures from data. Grounded in physical concepts of energy and equilibrium, these networks provided a new way of modeling complexity. Over time, they inspired a wide range of powerful techniques that now shape research both within and beyond physics.
By awarding them the Nobel Prize in Physics, the Academy has affirmed that the spirit of physics—seeking fundamental principles and using them to understand the world—can manifest in unexpected ways. The methods that Hopfield and Hinton developed show that physics-based thinking can illuminate not only the cosmos and subatomic particles, but also the patterns hidden in data and the processes of learning itself. In this sense, their work stays true to the deepest values of physics: using mathematical frameworks and careful reasoning to reveal order and meaning in a complex and often puzzling reality.


